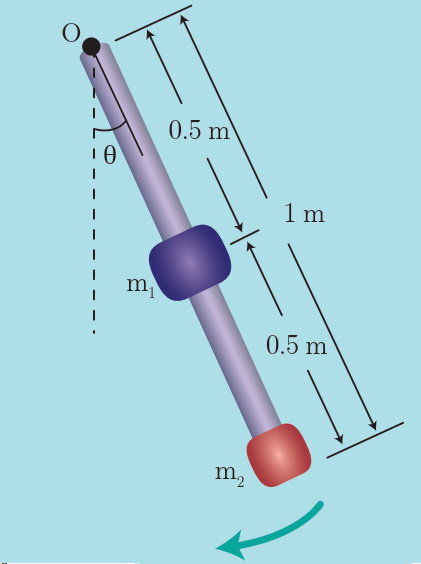
ساق شاقولية، مهملة الكتلة، طولها (L=1m)، نثبت في منتصفها كتلة نقطية (m1=0.4kg)، ونثبت في طرفها السفلي كتلة نقطية (m2=0.2kg)،

حساب دور هذا النواس في حالة السعات الزاوية الصغيرة:

T_o = 2.π √(I_∆ / (m1+m2).g.d

حساب عزم عطالة النواس: (الساق مهملة الكتلة)

I∆\o = m1.(L/2)² + m2.L2

I∆\o = 0.4*(1/2)² + 0.2*(1)² = 0.3 kg.m²

حساب d:

d = (m1.r1+m2.r2) / (m1+m2)

d = (m1.(L/2)+m2.L) / (m1+m2)

d = (0.4*(1/2)+0.2*1) / (0.4+0.2) = 2/3 m

T_o = 2.π √(I_∆ / (m1+m2).g.d

T_o = 2.π √(0.3 / (0.4+0.2)*10*(2/3)

T_o = √3 s

v_m2 = ω.L

v_c = ω.d

v_c / v_m2 = (ω.d) / (ω.L) = d/L

(4π/3√3) / (v_m2) = (2/3)/1

v_m2 = 2π/√3 m/s

نطبق نظرية الطاقة الحركية بين الوضعين:

الأول المطال الزاوي الأعظمي (θ1=θmax):

الثاني المرور بالشاقول (θ2=0):

∆Ek = ∑W_F

Ek2 - Ek1 = W_W + W_R

1/2*I_∆.ω² - 0 = (m1+m2).g.h + 0

h = l.(1 - cos θmax)

W_R = 0                   (لأن نقطة تأثيرها لا تنتقل)

1/2*I_∆.(v_c/d)² = (m1+m2).g.d.(1-cosθmax)

1/2*0.3*((4π/3√3)/(2/3))² = (0.4+0.2)*10*(2/3)*(1-cosθmax)

cosθmax = 1/2

θmax = π/3 rad