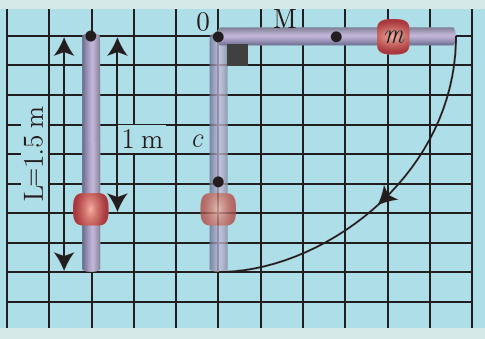
يتألف نواس ثقلي مركب من ساق شاقولية متجانسة، كتلتها (0.5kg)، طولها (1.5m)، يمكنها أن تنوس حول محور أفقي مار من طرفها العلوي،

حساب دور هذا النواس في حالة السعات الزاوية الصغيرة:

T_o = 2.π √(I_∆ / (m'+M).g.d

حساب عزم عطالة النواس:

عزم عطالة الساق حسب نظرية هايغنز:

I_∆\o = I_∆\c + M.d'²

I_∆\o = 1/12*M.L² + M.(L/2)² = 1/3*M.L² = 1/3*0.5*(1.5)²  = 0.375 Kg.m²

عزم عطالة الكتلة النقطية :

I_∆m' = m'.r'² = 0.5*(1)² = 0.5 kg.m²

عزم عطالة جملة النواس:

I_∆ = 0.375 + 0.5 = 0.875 kg.m²

حساب d:

d = (M.r1 + m'.r'2) / (M+m')

d = (M.(L/2) + m.r) / (M+m)

d = (0.5*0.75 + 0.5*1) / (0.5+0.5) = 0.875 m

T_o = 2.π √(0.875 / (0.5+0.5)*10*0.875 = 2 s

نطبق نظرية الطاقة الحركية بين الوضعين:

الأول المطال الزاوي الأعظمي (θ1=θmax):

الثاني المرور بالشاقول (θ2=0):

∆Ek = ∑W_F

Ek2 - Ek1 = W_F + W_R

Ek - 0 = (M+m').g.h + 0

W_R = 0                   (لأن نقطة التأثير لا تنتقل)

Ek  = (M+m').g.h

h = d

Ek = (M+m').g.d

Ek = (0.5+0.5)*10*0.875 = 8.75 J

Ek = 1/2*I_∆.ω²

السرعة الزاوية عند المرور بالشاقول:

ω = √2Ek/I_∆  = √(2*8.75)/(0.875) = √20 = 2√5 rad/s

السرعة الخطية عند المرور بالشاقول:

v = ω.r = 2√5*1 = 2√5 m/s