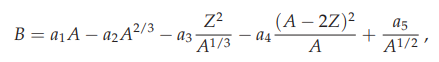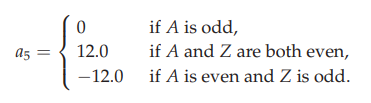حساب الصيغة شبه التجريبية للجزيئات الكيميائية باستخدام بلغة البرمجة Python

  • برمجة بايثون
  • فيزياء

2.10: في الفيزياء النووية، الصيغة شبه التجريبية لحساب الكتلة هي صيغة لحساب طاقة الربط النووية التقريبية B لنواة ذرية عددها الذري هو Z وعددها الكتلي هو A، هي:

 

حيث أن وحدة القياس هي meV، الثوابت في المعادلة هي:  a1 = 15.67, a2 = 17.23, a3 = 0.75, a4 = 93.2 والثابت a5 يحسب كالتالي: 

a) اكتب برنامجاً يأخذ مدخلاً القيم التالية: A و Z، والمخرجات هي طاقة الربط للذرة. استخدم البرنامج لحساب طاقة الربط لذرة عددها الذري هو 58 وعددها الكتلي هو 28 (ملوحظة: الإجابة الصحيحة هي 490MeV).

 

b) قم بتعديل برنامجك ليقوم بطباعة طاقة الربط الكلية لكل جزيء ذري B/A.

 

c) قم بتعديل برنامجك لكي يأخذ مدخلاً قيمة واحدة هي العدد الذري Z ومن ثم تقوم بالتحقق من جميع الأعداد من A=Z إلى A=3Z لإيجاد قيمة A التي تجعل طاقة الربط أقصى ما يمكن لكل جزيء ذري. ستكون هذه النواة هي الأكثر استقراراً. قم بطباعة القيمة A لهذه الذرة وقيمة طاقة الربط لكل جزيء بها.

 

2.10: In nuclear physics, the semi-empirical mass formula is a formula for calculating the approximate nuclear binding energy B of an atomic nucleus with atomic number Z and mass number A:

where, in units of millions of electron volts, the constants are a1 = 15.67, a2 = 17.23, a3 = 0.75, a4 = 93.2, and

 

a) Write a program that takes as its input the values of A and Z, and prints out the binding energy for the corresponding atom. Use your program to find the binding energy of an atom with A = 58 and Z = 28. (Hint: The correct answer is around 490 MeV.)

b) Modify your program to print out not the total binding energy B, but the binding energy per nucleon, which is B/A.

c) Now modify your program so that it takes as input just a single value of the atomic number Z and then goes through all values of A from A = Z to A = 3Z, to find the one that has the largest binding energy per nucleon. This is the most stable nucleus with the given atomic number. Have your program print out the value of A for this most stable nucleus and the value of the binding energy per nucleon. 

 

book name: Computational Physics

chapter: 2

author : Mark Newman

 

الأجوبة

a) 

import numpy as np
import math
a= 58
z=28
a1= 15.67
a2= 17.23
a3= 0.75
a4= 93.2
if z%2==0 and a-z%2==0: 
  a5= 12.00
elif z%2!=0 and a-z%2!=0:
  a5=-12.00
else: 
  a5= 0 
B= a1*a 
arr= [a]
ar=np.cbrt(arr)
for i in ar : 
  a13=i
 
B=B- (a2*a13*a13)
B=B- ((a3*z*z) /a13)
B=B- ((a4*(a-(2*z)) * (a-(2*z)))/a)
a12= math.sqrt(a)
B=B+(a5/a12)
print( "Atomic number, z=",z)
print( "Mass number, A=",a)
print (" Approximate nuclear binding energy is calculated as",B)

 

b) 

import numpy as np
import math
a= 58
z=28
a1= 15.67
a2= 17.23
a3= 0.75
a4= 93.2
if z%2==0 and a-z%2==0: 
  a5= 12.00
elif z%2!=0 and a-z%2!=0:
  a5=-12.00
else: 
  a5= 0 
B= a1*a 
arr= [a]
ar=np.cbrt(arr)
for i in ar : 
  a13=i
 
B=B- (a2*a13*a13)
B=B- ((a3*z*z) /a13)
B=B- ((a4*(a-(2*z)) * (a-(2*z)))/a)
a12= math.sqrt(a)
B=B+(a5/a12)
print( "Atomic number, z=",z)
print( "Mass number, A=",a)
print (" Approximate nuclear binding energy is calculated as",B/a)

c)

Z=int(input ("enter the value of z"))
al=15.67
a2=17.23
a3=0.75
a4=93.2 
lbn=0
lba=0
for a in range(Z,3*Z):
  if(a%2!=0):
    a5=0
  elif(a%2==0 and Z%2==0):
    a5=12.5
  else:
    a5=-12.0

b=al*a-a2*(a**(2/3))-a3*((Z**2)/(a**(1/3) ))-a4*(((a-2*Z)**2)/a)+a5/(a**(1/2))
epn=b/a
if(epn>lbn):
  lbn=epn
  lba=a
  print("For the most stable nucleon A is = ",a+1,"and the energy per nucleon is =",lbn,"MeV")

 

سجل الدخول لتستطيع الإجابة
هل كان المحتوى مفيد؟

0 نعم

0 لا

أسئلة مشابهة

حساب المعادلات ذات الحدين باستخدام لغة البرمجة Python
حساب ارتفاع القمر الصناعي باستخدام لغة البرمجة Python
حساب وقت سقوط كرة من أعلى برج باستخدام لغة البرمجة Python
حساب السنوات الضوئية لمركبة فضائية باستخدام لغة البرمجة Python

القوائم الدراسية التي ينتمي لها السؤال

معلومات ذات صلة

تبحث عن مدرس اونلاين؟

ابحث عن مدرسك
محتاج مساعدة باختيار المدرس الافضل؟ تواصل مع فريقنا الان لمساعدتك بتأمين افضل مدرس
ماهو التخصص الذي تبحث عنه؟
اكتب هنا...