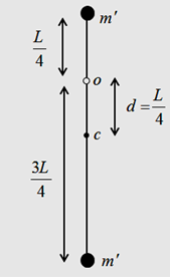
يتألف نواس ثقلي من ساق شاقولية، مهملة الكتلة طولها (L)، تحمل في كل من طرفيها كتلة نقطية ('m)، نعلق الجملة بمحور دوران أفقي يبعد (L/4)

استنتاج التابع الزمني للمطال الزاوي انطلاقاً من شكله العام: إيجاد ثوابت الحركة (θmax,ωo, ϕ)

θ = θmax.cos(ω_o.t + ϕ)

السعة الزاوية:

θmax= 1/2π rad

لأن الساق تركت دون سرعة ابتدائية.

النبض الخاص:

ωo =2π/To = 2π/2.5 = 4π/5 rad/s

لإيجاد الطور البتدائي نعوض شروط البدء في التابع الزمني (t=0,Xmax=1/2π rad):

1/2π = 1/2π.cos(0+ϕ)

cosϕ = 1

ϕ = 0 rad

نعوض ثوابت الحركة في التابع الزمني للمطال الزاوي:

θ = 1/2π.cos(4π/5.t)

حساب دور هذا النواس في حالة السعات الزاوية الصغيرة:

To = 2.π √I∆/m.g.d

حساب عزم عطالة النواس: (الساق مهملة الكتلة)

I_∆\o = m'.(L/4)² + m'.(3L/4)² = 10/16 m'.L²

حساب d:

d = ( m'.(3L/4) - m'.(L/4) ) / (m'+m')

d = m'.(L/2) / 2m'

d = L/4

To = 2.π √( ((10/16).m'.L²) / (2m'.g.(L/4))

To = 2.π √(5L) / (4g)

L = (To².g) / (5π²)

L = ((2.5)²*10) / (5*10) = 1.25 m

ω_max = ω₀.θ_max

ω_max = 4π/5 * 1/2π

ω_max = 0.4 rad/s

بعد انفصال الكتلة السفلية تصبح كتلة النواس m وعزم عطالته (I_∆\o= m(L/4)²) و (d=L/4)

To = 2π √(I_∆) / (m'.g.d)

To = 2π √(m'(L/4)²) / (m'.g.(L/4))

To = 2π √L/4g

To = 2π √1.25/4*10

To = √5/2 s