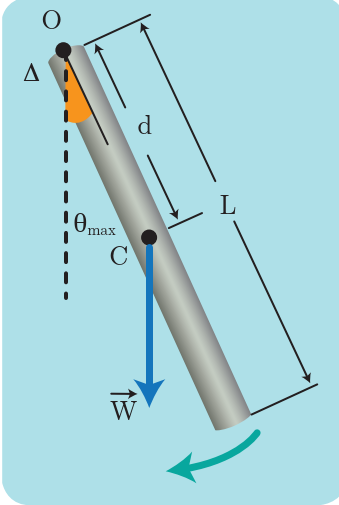
نواس ثقلي مؤلف من ساق متجانسة طولها (L=0.375m) وكتلتها M معلقة من طرفها العلوي بمحور أفقي عمودي على مستويها الشاقولي
- فيزياء
- 2021-05-21
- HalaHamid
نواس ثقلي مؤلف من ساق متجانسة طولها (L=0.375m) وكتلتها M معلقة من طرفها العلوي بمحور أفقي عمودي على مستويها الشاقولي، نزيح الساق عن موضع توازنها الشاقولي زاوية صغيرة (θ<14°) ونتركها دون سرعة ابتدائية. استنتج العلاقة المحددة للدور الخاص انطلاقاً من العلاقة العامة للدور الخاص للنواس الثقلي المركب، ثم احسب قيمتها علماً أن عزم عطالة الساق حول محور عمودي على مستويها ومار من مركز عطالتها (I∆/c = 1/2 ML2).
الأجوبة
يعطى دور النواس الثقلي بالعلاقة:
To = 2.π √(I∆ / m.g.d)
لإيجاد عزم عطالة الساق حول المحور المار من O:
نطبق نظرية هايغنر:
I∆ = I∆/c + M.d2
d = L/2
I∆ = 1/12*M.L2 + M.(L/2)2 = 1/3*M.L2
نعوض في علاقة الدور:
To = 2.π √((1/3*M.L2) / (M.g.L/2))
To = 2.π √(2L / 3g)
To = 2.π √(2*0.375 / 3*10) = 1 S
أسئلة مشابهة
القوائم الدراسية التي ينتمي لها السؤال