Find the area between the curves y=sin⁡x and y=cos⁡x on [0,2π].

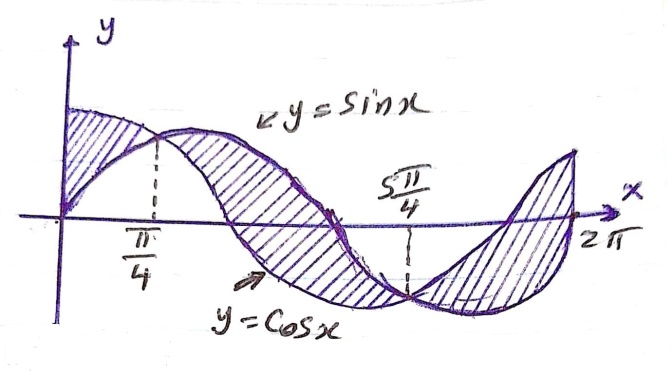
Solving the equations of the curves to get:
sin⁡x=cos⁡x   →sin⁡x/cos⁡x =tan⁡x=1 ,cos⁡x≠0
∴x=π/4   or  x=5π/4
Thus, the required area is:
A=∫_0^(π⁄4)〖(cos⁡x-sin⁡x)〗 dx+∫_(π⁄4)^(5π⁄4)〖(sin⁡x-cos⁡x)〗 dx+∫_(5π⁄4)^2π〖(cos⁡x-sin⁡x)〗 dx
=[sin⁡x+cos⁡x ]_0^(π⁄4)+[〖-cos〗⁡x-sin⁡x ]_(π⁄4)^(5π⁄4)+[sin⁡x+cos⁡x ]_(5π⁄4)^2π
=(sin⁡〖π/4〗+cos⁡〖π/4〗 )-1+(-cos⁡〖5π/4〗-sin⁡〖5π/4〗 )-(-cos⁡〖π/4〗-sin⁡〖π/4〗 )+(sin⁡2π+cos⁡2π )-(sin⁡〖5π/4〗+cos⁡〖5π/4〗 )
=1/√2+1/√2-1+(1/√2+1/√2)+(1/√2+1/√2)+1+1/√2+1/√2=8/√2=4√2   square units