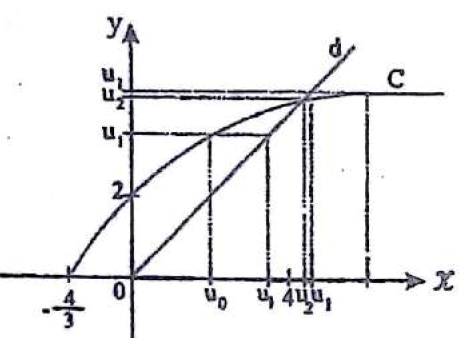
المتتالية (Un)n≥0 معرفة وفق: U0 > -4/3 Un+1 = √4+3Un هل هذه النتيجة صحيحة عندما -4/3<U0<4

F(x) = √4+3x

y=x

√4+3x=x

X2-3x-4=0

(x-4)(x+1) = 0

X = -1        (مرفوض)

X = 4

Y = 4

وC وd يتقاطعان في النقطة (4,4) من أجل U0=6 نجد:

U1 = √4+3Un = 4.69

من أجل U1=√22 نجد:

U2 = √4+3√22 = 4.25

يبدو أن المتتالية متناقصة.

إن جميه حدود المتتالية موجبة لأن:

Un+1 = √4+3Un > 0

4 + 3Un > 4

Un+1 = √4+3Un > 2

فالمتتالية محدودة من الأدنى بالعدد 2.

لنبرهن أن المتتالية متناقصة أي لنبرهن أن:

Un+1 < Un

المتراجحة صحيحة من أجل n=0 وn=1 وn=2 كما لاحظنا سابقاً لنفترض أنها صحيحة من أجل n أي Un+1<Un ولنبرهن على صحتها من اجل n+1 أي لنبرهن أن Un+2<Un+1 من الفرض حيث Un+1<Un صحيحة نجد:

3Un+1 < 3Un

4 + 3Un+1 < 4+3Un

√4+3Un+1 < √4+3Un

Un+2 < Un+1

والمتراجحة صحيحة من أجل n+1 فهي صحيحة أياً يكن n وبالتالي فالمتتالية متناقصة.

المتتالية متناقصة ومحدودة من الأدنى بالعدد 2 فهي متقاربة.

إن العدد 2 حد قاصر للمتتالية وليس من الضروري أن يكون نهايتها.

يبدو من الشكل في حالة 4<Un المتتالية متناقصة ونهايتها 4.

وإذا كانت Un<4 فالمتتالية متزايدة ونهايتها 4 وفي الحالتين تكون المتتالية محدودة بالعدد 4 وهو نهايتها وهي متقاربة في الحالتين.

فإذا كانت:

Lim (Un) n→+∞ = x

√4+3x = x

X2-3x-4 = 0

(x+1)(x-4) = 0

(x=-1) مرفوض

لأن حدود المتتالية موجبة ونجد أن x=4 هو نهايتها ويمكن ان نقو ان Un عندما U0>4 والمتتالية Un عندما Un<4 إنهما متجاورتان لأن الأول متناقصة والثانية متزايدة ولهما ذات النهاية 4 وهما متقاربتان.