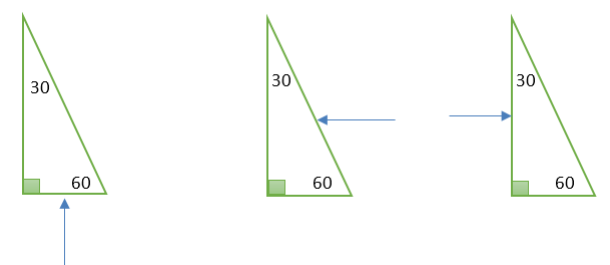
تتبع مسار الشعاع الضوئي الوارد على كل موشور في الشكل في الأسفل، وعين زاوية البروز 2 theta في كل حالة موضحاً السبب

يرد الشعاع الضوئي على الوجه الأول عمودياً على السطح الفاصل فينفذ دون انحراف داخلاً الموشور وتكون:

Θ1 = β = 0

نحسب الزاوية الحرجة باستخدام العلاقة:

sin Θc =1/n = 1/1.5 = 0.667

Θc =42º

وهذه الزاوية الحرجة هي لجميع الحالات لأن الموشور ذاته.

يرد الشعاع الضوئي على الوجه الثاني بزاوية (‘=30ºβ) على السطح الفاصل وهذه الزاوية أصغر من الزاوية الحرجة فإنه ينكسر مبتعداً عن الناظم، ولحساب زاوية البروز نطبق قانون سنل:

n.sinβ’ = sinΘ2

1.5*sin(30) = sinΘ2

sin Θ2 = 0.75

Θ2 = 49º

في الشكل الآتي: نرسم الناظم على السطح الأول فتكون زاوية الورود (θ1=30º)

الشعاع الضوئي ينكسر مقترباً من الناظم وتكون زاوية الانكسار (=19ºβ)

Β’ = Φ – β = 30º - 19º = 11º

يرد الشعاع الضوئي على الوجه الثاني بزاوي أصغر من الزاوية الحرجة فإنه ينكسر مبتعداً عن الناظم، ولحساب زاوية البروز نطبق قانون سنل:

n.sinβ’ = sinΘ2

1.5*sin(11) = sinΘ2

sin Θ2 = 0.286

Θ2 = 17º

في هذا الشكل يرد الشعاع الضوئي على الوجه الأول عمودياً على السطح الفاصل فينفذ دون انحراف داخلاً الموشور وتكون:

Θ1 = β = 0

يرد الشعاع الضوئي على الوجه الثاني بزاوية (‘=60ºβ) على السطح الفاصل وهذه الزاوية أكبر من الزاوية الحرجة فإنه ينعكس داخل الموشور، وتكون

زاوية الورود = زاوية الإنعكاس.

يرد الشعاع الضوئي على الوجه الثالث بعد الانعكاس فيصنع مع الناظم على السطح الفاصل زاوية تساوي (‘=30ºβ) أصغر من الزاوية الحرجة فإنه ينكسر مبتعداً عن الناظم، ولحساب زاوية البروز نطبق قانون سنل:

n.sinβ’ = sinΘ2

1.5*sin(30) = sinΘ2

sin Θ2 = 0.75

Θ2 = 49º