سكتان نحاسيتان متوازيتان تميل كل منهما على الافق بزاوية 45 درجة تستند إليهما ساق نحاسية طولها 40cm تخضع لتأثير حقل مغناطيسي منتظم
- فيزياء
- 2021-05-22
- HalaHamid
سكتان نحاسيتان متوازيتان تميل كل منهما على الافق بزاوية 45 درجة , تستند إليهما ساق نحاسية طولها 40cm تخضع لتأثير حقل مغناطيسي منتظم شاقولي شدته 0.8T نغلق الدارة ثم تترك لتنزلق دون احتكاك بسرعة ثابتة قيمتها 2m/s. والمطلوب:
- بين أنه تنشأ قوة كهرطيسي تعيق حركة الساق.
- استنتج العلاقة المحددة للمقاومة الكلية للدارة ثم احسب قيمتها اذا كانت شدة التيار المتحرض المتولد فيها √2A.
- استنتج العلاقة المحددة لكتلة الساق ثم احسب قيمتها.
الأجوبة
عند تحريك الساق بسرعة ثابتة، عمودياً على خطوط الحقل المغناطيسي فإّن كل إلكترون حّر في الساق سيتحرك بهذه السرعة وسطيا ، ومع خضوعها لتأثير الحقل المغناطيسي المنتظم فإّنه يخضع لتأثير القوة مغناطيسية (F=-ev^B) وبتأثير هذه القّوة تتحرك الإلكترونات الحرة عبر الدارة فيتوّلد تيار كهربائي متحّرض ينتج أفعالاً تعاكس السبب الذي أدى إلى حدوثه فتنشأ القوة الكهرطيسية معاكسة جهة حركة الساق.
استنتاج العالقة المحّددة للمقاومة الكلية للدارة:
- حركة الساق بسرعة ثابتة v خلال الفاصل الزمني t∆ تنقلها مسافة
∆x = v∆t
- فتتغير مساحة السطح الذي تخترقه خطوط الحقل المغناطيسي بمقدار
∆s = L∆x = Lv∆t
- ويتغّير التدّفق المغناطيسي الذي يجتاز الدارة بمقدار.
∆Φ = B.∆s.cosa = B.L.v.∆t.cosa
- فتتوّلد قوة محّركة كهربائية متحّرضة قيمتها المطلقة.
ε = | ∆Φ/∆t | = B.L.v.cosa
فيتوّلد تيار كهربائي متحّرض:
i = ε/R = B.L.v.cosa
المقاومة الكلية:
R = (B.L.v.cosa)/i
R = (0.8*40*10-2*2*(1/√2))/√2
R = 32*10-2 Ω
استنتاج العلاقة المحددة لكتلة الساق :
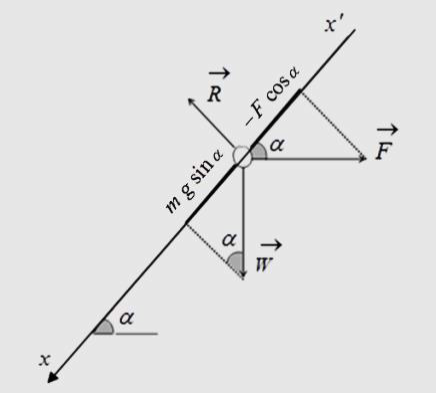
جملة المقارنة: خارجية. الجملة المدروسة: الساق المتوازنة.
القوى الخارجية المؤثرة:
W: ثقل الساق
F: القوة الكهرطيسية
R: رد فعل السكتين
W + F + R = 0
بالإسقاط على x'x:
m.g.sina - F.cosa + 0 = 0
m = (F/g).tana
m = (i.L.B.sin(π/2))/g *tana
m = (√2*40*10-2*0.8*1*1)/10
m = 32√2*10-3 kg
أسئلة مشابهة
القوائم الدراسية التي ينتمي لها السؤال